Cálculo de Reactancias y Resistencias en Paralelo: Teorema de Pitágoras
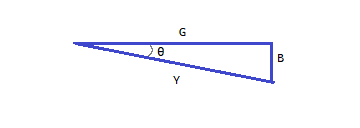
En circuitos de corriente alterna (CA) con componentes en paralelo, la admitancia total se puede calcular utilizando el teorema de Pitágoras. La conductancia y la susceptancia forman los catetos de un triángulo rectángulo, siendo la admitancia la hipotenusa.
Y = √(G² + B²)
Fórmulas derivadas:
G = √(Y² - B²)
B = √(Y² - G²)
θ = arctan(B/G)
G = Y · cos(θ)
B = Y · sin(θ)
|Z| = 1/Y
R = G / (G² + B²)
X = -B / (G² + B²)
|
Y = admitancia total
G = conductancia
B= susceptancia |
Características:
- La admitancia (Y) es la facilidad con la que la corriente fluye en un circuito CA.
- La conductancia (G) es la parte real de la admitancia.
- La susceptancia (B) es la parte imaginaria de la admitancia.
- El ángulo de fase (θ) se puede calcular como θ = arctan(B/G).
|
 |
Ejemplo de cálculo:
Calcular la admitancia total de un circuito en paralelo con una conductancia de 0.2 S y una susceptancia capacitiva de 0.15 S.
Solución :
Y = √(G² + B²)
Y = √(0.2² + 0.15²)
Y = √(0.04 + 0.0225)
Y = √0.0625 = 0.25 S
Ángulo de fase: θ = arctan(B/G) = arctan(0.15/0.2) ≈ 36.87°
Para convertir la admitancia a impedancia:
Z = 1/Y = 1/0.25 = 4 Ω